2.7 La Stima del Rendimento Finale







In un modello quantitativo statistico, il rendimento di un investimento rappresenta la variabile dipendente, mentre il tempo e il rischio sono le variabili indipendenti. Ciò sta a significare che il rendimento dipende dal rischio e dal tempo. Le tre variabili sono legate da una relazione statistico-probabilistica che trova il suo fondamento nelle teorie dell'efficienza dei mercati e che consente di analizzare in maniera razionale le opportunità che potrebbero essere colte dall'investimento esaminato. Le relazioni tra tempo, rischio e rendimento possono essere descritte in termini quantitativi, utilizzando strumenti statistici opportuni. Per avere una idea concreta delle molteplici relazioni che si possono stabilire tra le variabili, si può osservare il grafico seguente:

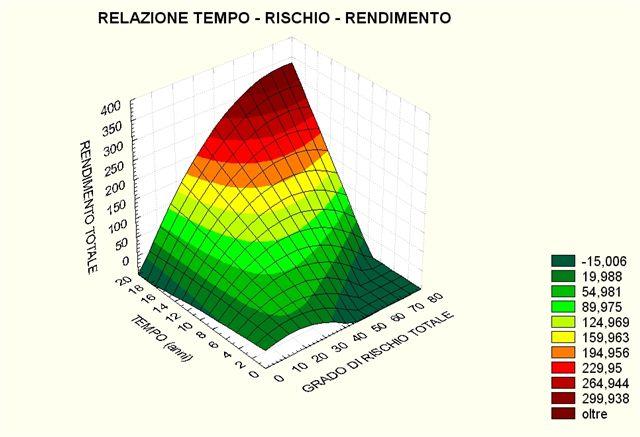Il grafico descrive un insieme di opportunità di investimento derivate dalla combinazione di tre mercati di riferimento: monetario (Indice BOT), obbligazionario internazionale (Indice JP Morgan Globale) ed azionario internazionale (Indice Msci World). L'informazione che se ne ricava è particolarmente illuminante. La superficie all'interno del piano tridimensionale figura il rendimento assoluto ottenibile in funzione del tempo (per comodità visiva, espresso in anni) ed il rischio (deviazione standard calcolata in funzione del tempo). Come si potrà notare, l'area più scura in basso evidenzia due zone di rendimento negativo. Infatti, se ci si sposta sull'asse temporale a rischio quasi nullo si osserverà che dall'ottavo anno in poi tale zona scura compare ed aumenta. Ciò sta a dimostrare il distruttivo effetto dell'inflazione a lungo termine su investimenti con un grado di rischio molto basso. Se invece ci si sposta sull'asse del rischio con orizzonti temporali molto brevi, l'area di rendimento negativo ammonisce di non assumere un grado di rischio superiore ad una certa soglia (da 40 in poi) prima di 6-8 anni. Ciò dimostra l'effetto negativo nell'assunzione di un rischio decisamente alto in tempi relativamente brevi. Infine, la particolare conformazione della superficie sostanzia, in termini grafici, la necessità di individuare investimenti che consentano, dato un tempo ed un rischio adeguato, di rendere massima la prospettiva di rendimento ottenibile. Ma non basta. Proprio per gestire l'aleatorietà dei mercati, è necessario che il rendimento possa essere espresso in termini di probabilità oggettiva del suo raggiungimento. Il termine "oggettiva" sta ad indicare che la quantificazione delle probabilità deve essere frutto di un calcolo basato su dati e su una solida teoria di riferimento (v. approfondimento: la Random Walk Theory). Altrimenti, se la probabilità fosse espressa in conformità a considerazioni soggettive dell'operatore, questa potrebbe rappresentare solo una sua speranza o una motivazione di vendita. La traduzione del rischio in termini di probabilità oggettive di conseguire un rendimento è rappresentata dal grafico seguente.

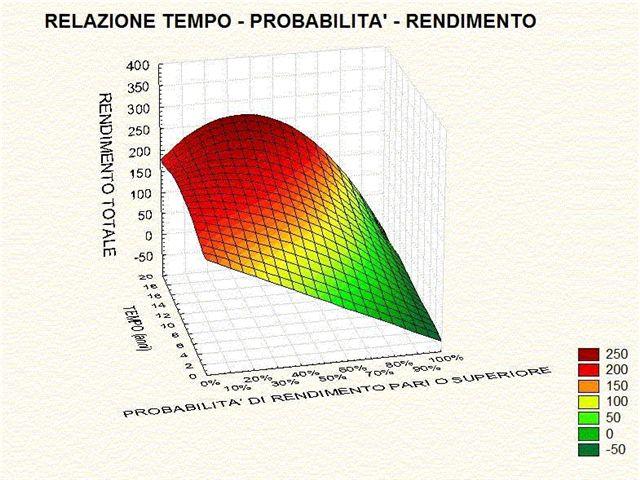La probabilità oggettiva fornisce un'indicazione di realizzabilità, o affidabilità, di conseguire un dato rendimento. Essa viene espressa in termini percentuali compresi tra lo 0% e il 100%. Lo 0% segnala che il rendimento non ha praticamente alcuna possibilità di realizzarsi, il 100% invece avvisa che l'acquisizione del rendimento è relativamente certa (la certezza statistica non esiste), mentre i valori intermedi indicano stati progressivi di maggiori possibilità di accadimento. Al fine di rendere più comprensibile e familiare il significato dei vari livelli di probabilità oggettive, sarà sufficiente fare riferimento a una esperienza che è nella vita quotidiana di ognuno: la conoscenza della statura delle persone. Su dati ISTAT 1994, sono state individuate le probabilità oggettive di estrarre a caso un individuo maggiorenne con statura uguale o superiore a un determinato valore. Dall'osservazione della figura seguente si evidenzia che la probabilità del 50% corrisponde all'estrazione casuale di una persona più alta di 167 cm.

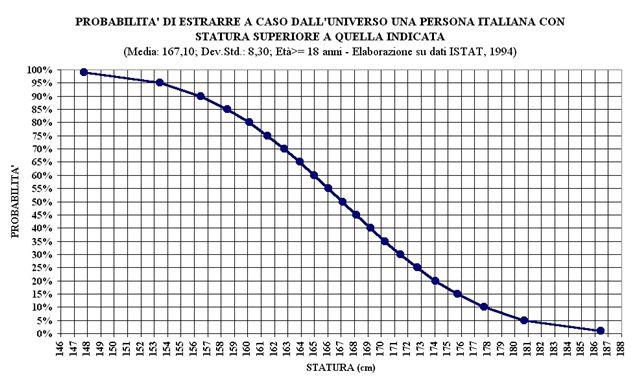Per esempio, la possibilità di realizzare una data performance reale con una probabilità del 95%, equivarrebbe ad incontrare casualmente un italiano maggiorenne con altezza superiore a 153 cm., mentre una probabilità dell'84% equivarrebbe ad un incontro casuale con un italiano maggiorenne di altezza superiore ad 159 cm. Questi confronti possono ben aiutare a comprendere il grado di affidabilità degli scenari e dei criteri oggettivi utilizzati nella valutazione del rendimento potenziale acquisibile. In Investment Profiler la Stima rendimento Finale rappresenta dunque la stima del rendimento atteso reale al Tempo Opportunità, espresso in termini percentuali rispetto all'importo investito. I valori definiscono un intervallo di normalità (stimati con probabilità pari all'84% e al 16%) entro il quale si attende che si posizioni il valore della tendenza centrale (p= 50%) a scadenza. Per una corretta interpretazione del valore delle stime statistiche è consigliabile fruire dell'approfondimento. I dati, confrontati con le altre indicazioni fornite, consentono di valutare oggettivamente la congruità del premio rispetto al tempo ed al rischio che si intende assumere ragionevolmente.

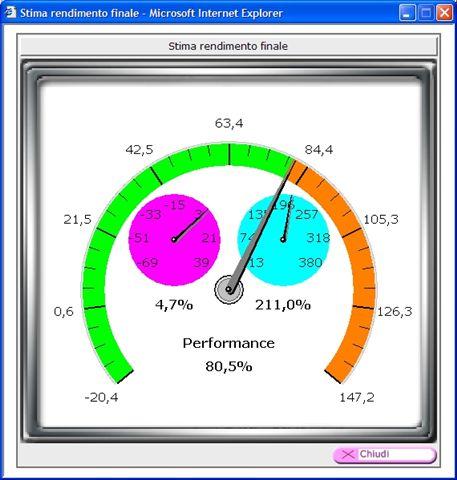La lancetta del misuratore indica la stima del rendimento dell'elemento esaminato ed è inserita all'interno del contatore i cui valori minimo-massimo si riferiscono agli elementi selezionati inizialmente come gamma di riferimento.





RWT & Montecarlo

La modalità di effettuare stime statistiche oggettive del profilo di rischio-rendimento utilizzando la più potente teoria relativa ai mercati di investimento e la più efficiente metodologia: Random Walk Theory e Metodo Montecarlo.




Il valore delle stime statistiche.

La certezza è solo un mito. La stima statistica come alternativa razionale.